1. Оптические двойные и физические двойные звезды. Двойные звезды бывают двух типов: оптические и физические. Например, Мицар и Алькор в созвездии Большой Медведицы видны невооруженным глазом, но они не просто проецируются рядом на небесной сфере. Это физическая двойная звезда, движущаяся вокруг общего центра масс. Их период обращения около 2 миллионов лет. Большинство звезд в двойных системах имеют более тесные орбиты с периодами обращения в сотни лет.
Например, α Близнецов (Кастор) состоит из двух компонентов (А и В), расстояние между которыми приблизительно 100 астрономических единиц. Эти компоненты также являются двойными, но их двойственность невозможно обнаружить визуально или фотографически. Она проявляется только в спектрах, где наблюдается периодическое раздвоение спектральных линий.
Двойственность тесных пар звезд также может быть выявлена через периодические изменения блеска. Если орбита двойной звезды проходит близко к направлению от наблюдателя к центру масс, то происходят затмения, когда одна звезда временно заслоняет другую. Эти звезды называются затменными переменными. Измерив амплитуду изменения блеска и интервал между максимумами, можно определить период изменения блеска звезды.
Кривая блеска затменной переменной звезды, как например β Персея (или Алголь), может быть использована для определения их радиусов.
2. Определение масс звезд из наблюдений двойных звезд. Формулы позволяют нам провести определение масс звезд в двойных системах. Формула связывает массы главной звезды (M1) и её спутника (M2) с периодом обращения спутника (P) и большой полуосью его орбиты (A):
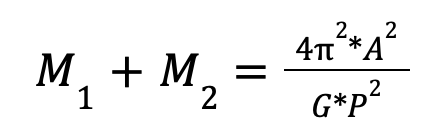
Если принять массу Солнца за единицу (M=1) и учесть, чтоT=1 год, a=1 а.е., то формула примет следующий вид:
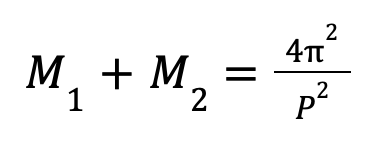
Величина A связана с годичным параллаксом звезды (π) и угловым расстоянием между компонентами (α) простым соотношением:
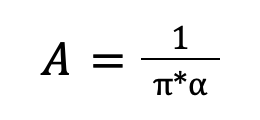
где a и π выражены в секундах дуги, а расстояние A — в астрономических единицах.
Учитывая равенство, формулу можно записать в виде:
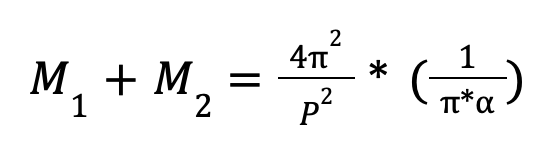
Эти уравнения позволяют нам определять массы звезд в двойных системах, используя наблюдения и измерения, такие как период обращения спутника и угловое расстояние между компонентами.
***
Пример 11. Процион (а Малого Пса) — двойная звезда, у которой период обращения спутника около 39 лет, а большая полуось орбиты 13 а. е. Какова сумма масс компонентов этой системы?
Так как мы знаем, что период обращения спутника P=39 лет, большая полуось орбиты A=13 а.е., а масса Солнца M=1, используем формулу:
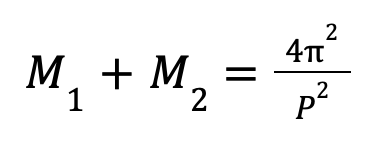
Подставим известные значения:
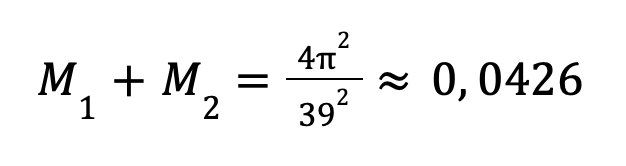
Так как масса Солнца равна 1, то массы компонентов Проциона можно выразить в солярных массах:
M1+M2 ≈ 0,0426M
Итак, сумма масс компонентов системы Процион составляет примерно 0.0426 солярных масс.
***
3. Невидимые спутники звезд. Великолепная звезда Сириус, венчающая наше зимнее небо, — двойная система, где яркая Сириус A тесно связана с массивным невидимым спутником, белым карликом Сириус B. Открытие этого спутника было результатом тщательного анализа аномалий в наблюдаемом движении Сириуса.
Тем не менее, не только карликовые звезды могут оказывать влияние на движение главной звезды. Ведь в роли спутников звезд могут выступать и планеты. Эту гипотезу предвосхищали великие мыслители прошлого. Особенно ярко и наглядно Джордано Бруно сформулировал идею о наличии планет у других звезд. К концу XX века ученым удалось обнаружить планеты у десятков звезд, находящихся на расстоянии десятков и сотен световых лет от нас.
Эти звезды, сопровождаемые крупными спутниками (планетами) или планетными системами, были обнаружены в созвездиях Лебедя, Пегаса, Андромеды, Большой Медведицы, Геркулеса, Волопаса и многих других. Открытие «внесолнечных» планет является одним из значимых доказательств того, что планетарные системы во Вселенной могут быть распространены. Особый интерес представляют те планетарные системы, которые сходны с солнечной системой нашего Солнца.













