1. Введение. Звезды разбросаны в пространстве на различных удалённостях от нас, и не существует никакой абсолютной «сферы звезд». Не существует неподвижных звезд — астрономические наблюдения подтверждают их движение. Скорость, с которой звезда перемещается в пространстве относительно Солнца, называется пространственной скоростью. Представим вектор пространственной скорости одной из звезд (см. рисунок 81) как сумму двух составляющих векторов. Одна из них (тангенциальная скорость) перпендикулярна лучу зрения (то есть направлению от звезды к наблюдателю), а другая направлена вдоль луча зрения (лучевая скорость). Тогда, согласно теореме Пифагора, модуль пространственной скорости определяется следующим образом:
|V| = √(V_t² + V_r²) (42)
Давайте рассмотрим методы вычисления модулей векторов V_t и V_r.
2. Собственные движения и тангенциальные скорости звезд. Уже в XVIII веке стало очевидно, что экваториальные координаты звезд изменяются в течение длительных временных промежутков. Это происходит из-за движения звезд в пространстве. Угловое перемещение звезды на небесной сфере за год называется собственным движением и измеряется в секундах дуги в год (обозначается как µ). Звезда Барнарда (в созвездии Змееносца) обладает наибольшим собственным движением, µ = 10,3˝. Зная µ, можно вычислить модуль тангенциальной скорости. Расстояние r до звезды соответствует годичному параллаксу звезды π. Если π выражено в радианах, то V_t = µ * r. Поэтому V_t = µ * a, где a = 1 а. е.
Так как 1 а. е. = 1,496∙10^8 км, а t_0 = 3,16∙10^7 секунд, тангенциальная скорость, выраженная в километрах в секунду, равна:
V_t (км/с) = µ * a (км) / t_0 (сек) (43)
3. Эффект Доплера и определение лучевых скоростей звезд. Лучевые скорости определяются по спектрам звезд с использованием эффекта Доплера. Этот эффект проявляется в смещении спектральных линий источника, приближающегося к наблюдателю, к фиолетовому концу спектра, а линий удаляющегося источника — к красному концу. Смещение зависит от скорости и направления движения. Формула для вычисления лучевых скоростей:
V_r = c * λ — λ_0 / λ_0 * c,
где c — скорость света, λ — длина волны, λ_0 — наблюдаемая длина волны. Таким образом, лучевая скорость удаляющегося источника выражается с плюсом, а приближающегося — с минусом.
Пример 9. В спектре звезды линия, соответствующая длине волны 5,5 * 10-4мм, смещена к фиолетовому концу спектра на 5,5 * 10-8 мм. Определить лучевую скорость звезды.
Для решения этой задачи используется формула для определения лучевой скорости с использованием эффекта Доплера:
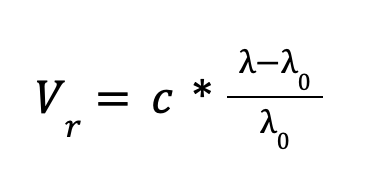
где:
- c — скорость света (3×1083×108 м/с)
- λ — наблюдаемая длина волны (5,5∙10^-4 мм, что равно 5,5×10−75,5×10−7 м)
- λ0 — исходная длина волны (5,5∙10^-4 мм, что равно 5,5×10−75,5×10−7 м)
Подставляем известные значения:
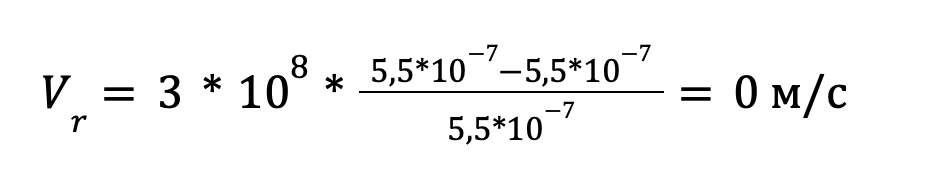
Таким образом, лучевая скорость звезды равна нулю.













